This article provides a brief analysis of the formula for calculating commutation noise frequency in brushless motors. Brushless motors operate in six different states, denoted by 1 and 0, representing the direction of current flow in the three-phase winding—1 for positive and 0 for negative. Positive current flows from the first end to the last end of the winding, while negative current flows from the last end to the first end.

A single motor unit of a brushless motor (either the stator or rotor with one pair of poles) exhibits six operational states within one cycle. Transitioning between adjacent states generates torque pulsations known as commutation torque ripple, affecting both the stator and rotor. As a brushless motor typically has four pairs of poles, there are a total of 4×6=24 operational states in one cycle. Hence, the formula for calculating the commutation torque ripple frequency (referred to as the commutation frequency) is derived as follows:

where:

• ( i ) is the frequency order, producing the commutation noise frequency in Hertz (Hz),

• ( k ) is the number of operational states corresponding to each pair of poles in one cycle of the stator or rotor

• ( p ) is the number of pole pairs in the brushless motor
• ( n ) is the motor speed in revolutions per minute (RPM).

As most brushless motors operate in the 6th state mentioned, the formula can be simplified to:

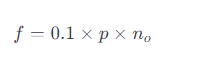
When the commutation frequency of a brushless motor matches or approaches any natural frequency of the motor system, noticeable vibrations and commutation noise are generated at the corresponding frequency.

This article provides a basic introduction to the formula for calculating the commutation noise frequency in brushless motors. Faradyi Motors focuses on research, development, and production of high-performance, high-quality brushless motors, DC servo motors, stepper motors, and related drive controllers in the global industrial automation field. It is a leading high-tech enterprise in China, providing advanced motion control technology solutions.